Research
My scientific research has been focused on soft condensed matter and biophysics. Keywords related to my research include non-equilibrium statistical physics, molecular and cellular biology, liquid crystals, active materials, complex fluids, bacterial locomotion, collective behavior, and spontaneous pattern formation.
In my research work, I use theoretical modeling, statistical data analysis, and a wide variety of computational techniques like simulations (Molecular Dynamics, Monte Carlo, Brownian Dynamics, Dissipative Particle Dynamics, Multi-particle Collision Dynamics), parallel high-performance computing (OpenMP, MPI, CUDA), and advanced visualization software.
Here is a short description for some of my research projects.
Collective behavior of self-propelled particles
Collective behavior is an intriguing aspects of many complex systems. The organized motion of bird flocks and fish schools are familiar macroscopic examples. Similarly in micro-scale, it is observed from bacterial colonies and sperm cells to human-made systems of propelled protein filaments and bimetallic nano-rods.
Studying the origin and mechanisms for such organized motion is important not only for understanding the behavior of different biological and synthetic systems, but also to control their properties for promising medical and industrial applications.
By means of computer modeling and analytical arguments, we study the collective behavior of self-propelled particles. We show that the phase transition of particles from random isotropic motion to organized “swarms” is a competition between self-propulsion, steric interaction, and environmental noise, and can be quantitatively predicted using a characteristic “gas density” for self-propelled particles.
isotropic suspension of rods with no propulsion |
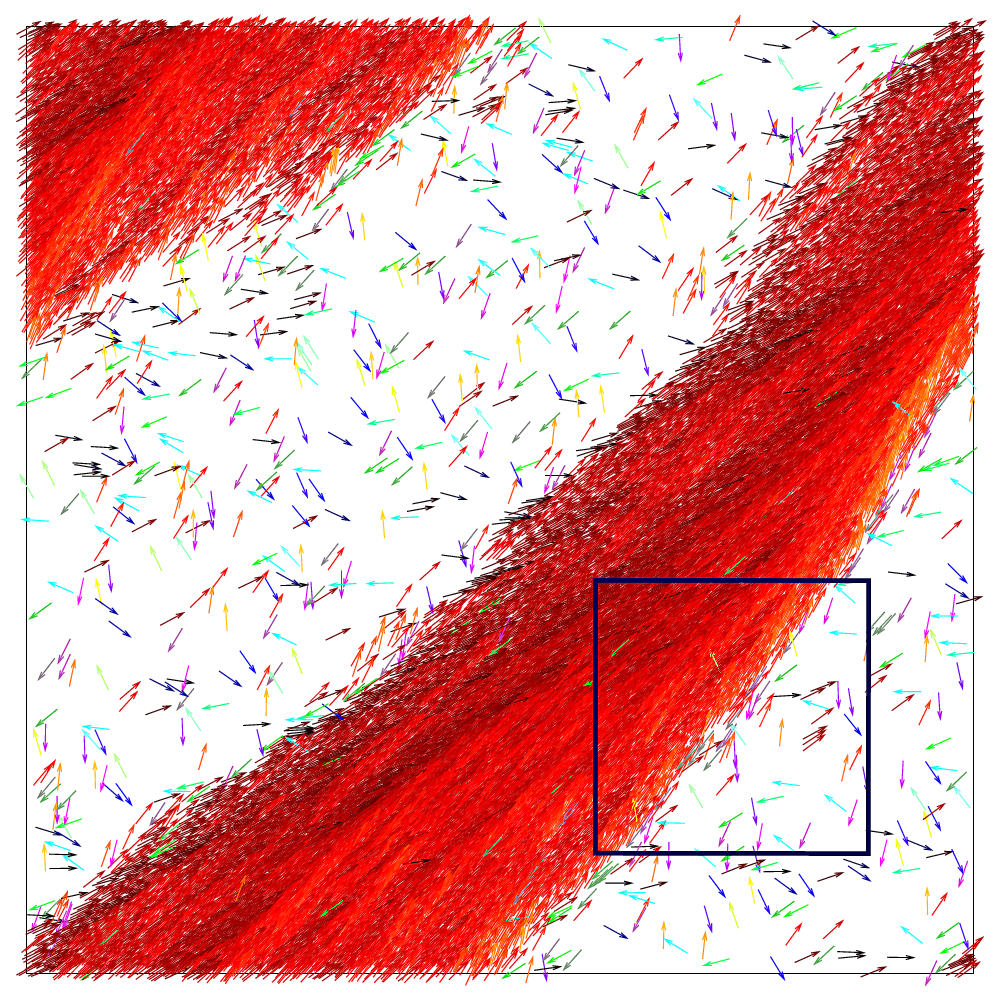
large cluster of self-propelled rods |
close up of a large cluster |
Videos
Related publication
-
Masoud Abkenar, Kristian Marx, Thorsten Auth, and Gerhard Gompper. Collective behavior of penetrable self-propelled rods in two dimensions. Physical Review E 88, no. 6 (2013): 062314.
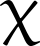
Generalized Onsager’s theory for isotropic-nematic transition of liquid crystals
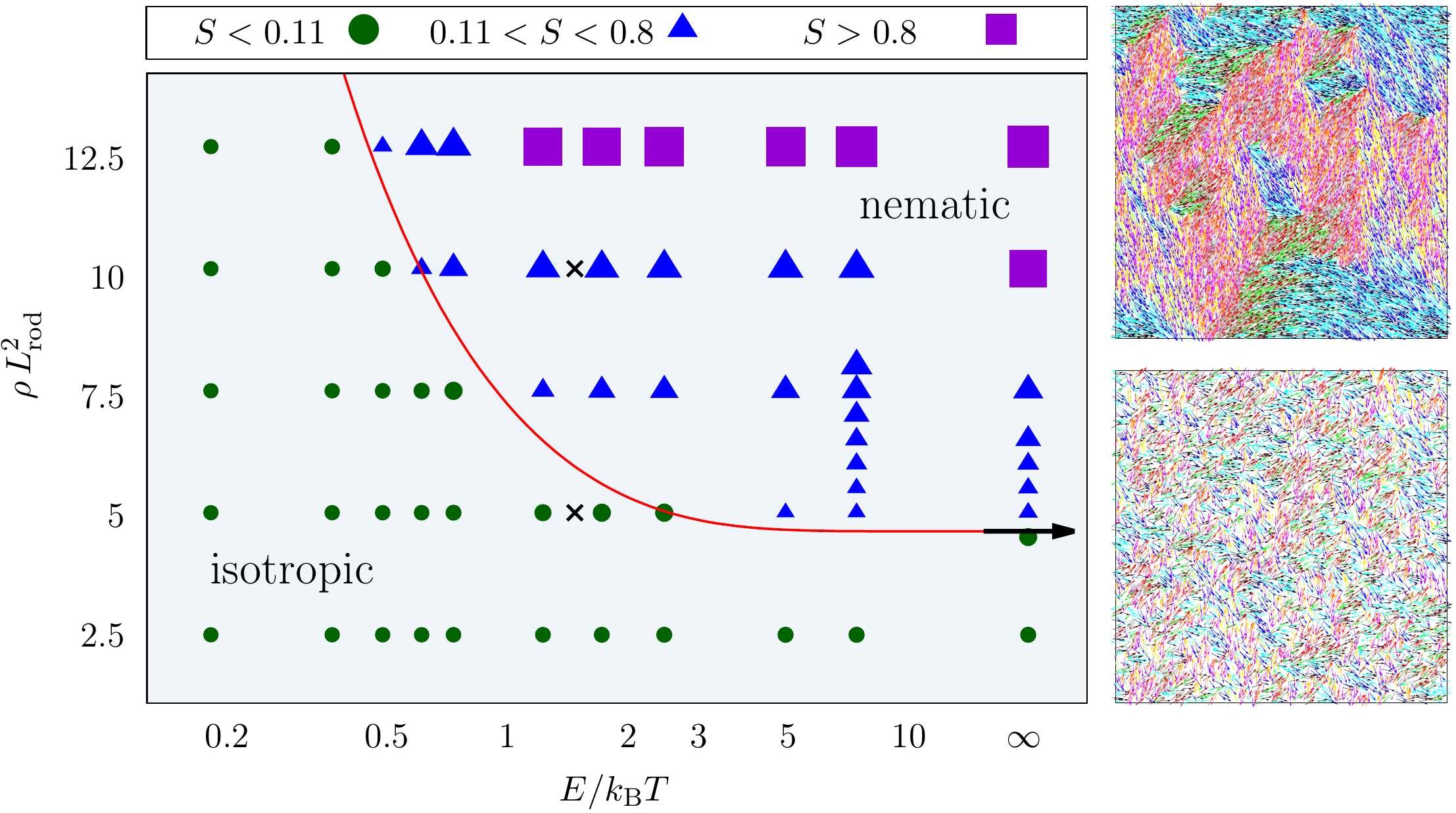
Suspensions of passive rod-like particles are isotropic for low densities and nematic for high densities. The critical density for the isotropic-nematic transition is given by Onsager’s theory. However, in quasi two-dimensions, where the rods are loosely bond to a substrate but can also occasionally intersect with an energy barrier E, this critical density is higher due to the weaker repulsion between the rods.
We have developed an analytical theory together with extensive Monte Carlo simulations to systematically study the state of the system for several values of density and energy barrier. With our generalized Onsager’s theory, the transition from isotropic state to nematic state occurs at
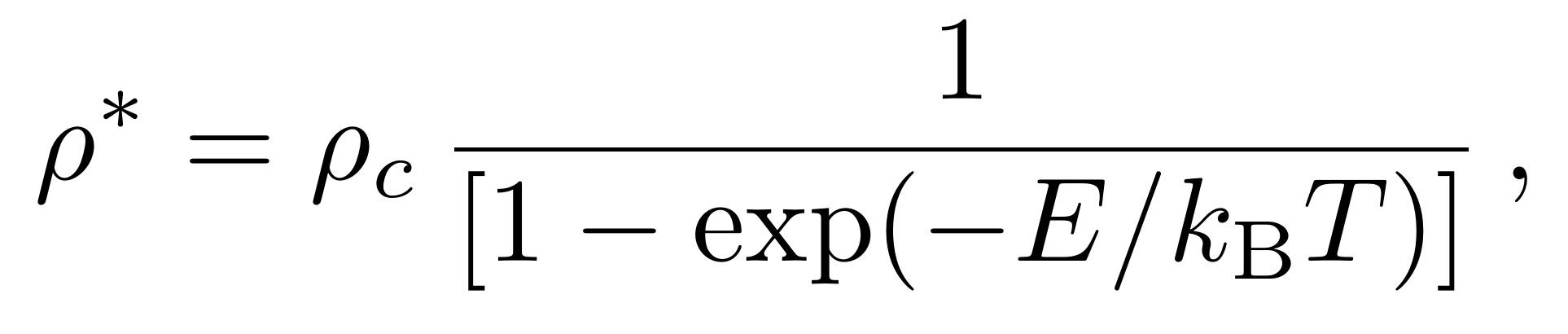
where
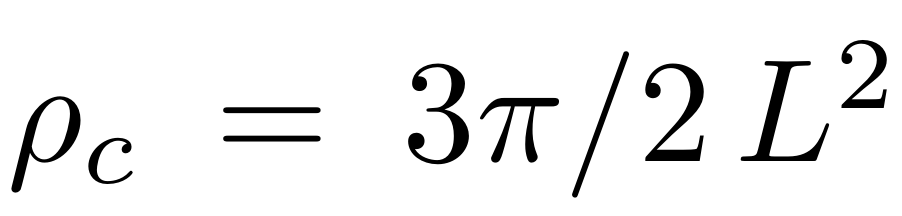 is the critical density given by Onsager’s theory for impenetrable rods.
We observe excellent agreement between our theory (without any fitting parameters) and the Monte-Carlo simulations.
is the critical density given by Onsager’s theory for impenetrable rods.
We observe excellent agreement between our theory (without any fitting parameters) and the Monte-Carlo simulations.
Related publication
-
Masoud Abkenar, Kristian Marx, Thorsten Auth, and Gerhard Gompper. Collective behavior of penetrable self-propelled rods in two dimensions. Physical Review E 88, no. 6 (2013): 062314.
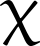
Dissociation of weak bonds under thermal fluctuations
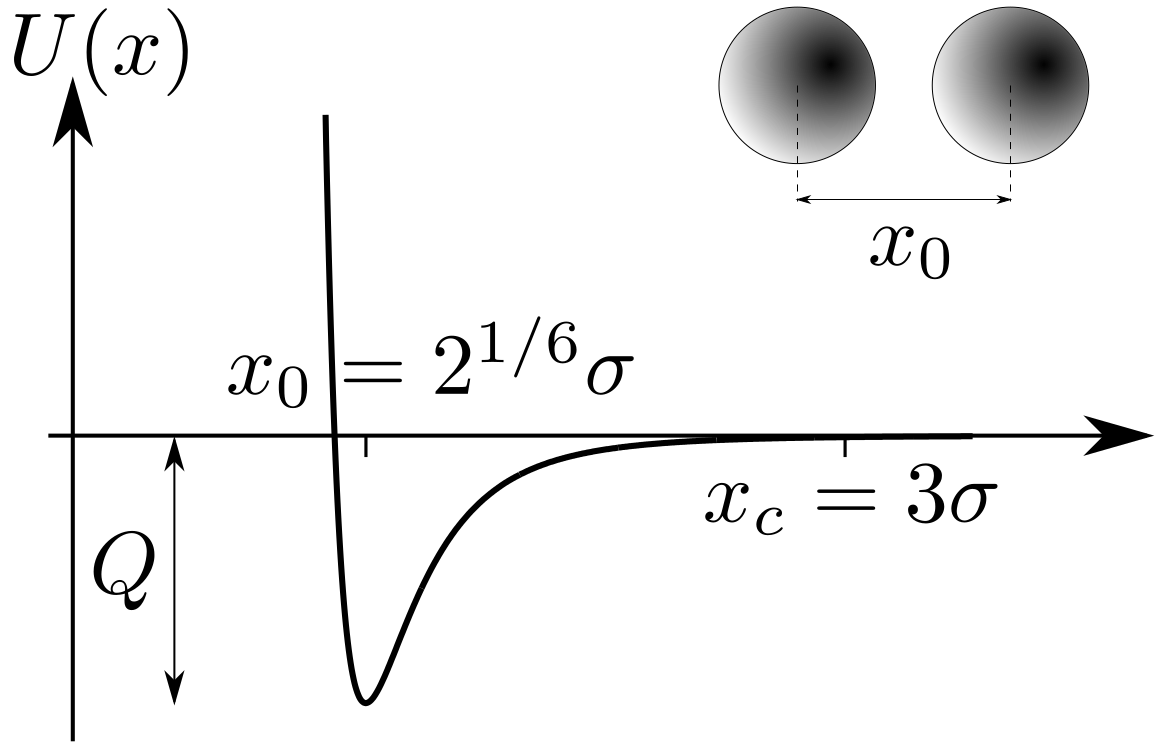
Formation of intermolecular bonds in thermally agitated environments is ubiquitous from biological to condensed matter physics. Examples include adsorption of particles to membranes (e.g. entrance of malaria virus into a red blood cell) and protein-ligand bindings. The energy gain upon forming the bond—the binding energy Q —determines the bond’s stability in an environment with thermal fluctuations. When the binding energy and thermal fluctuations are comparable, i.e., E ≡ Q/kB T ≈ 1, the bond can break on a relatively short time scale. Conversely, larger binding energies mean increased stability and longer mean dissociation times.
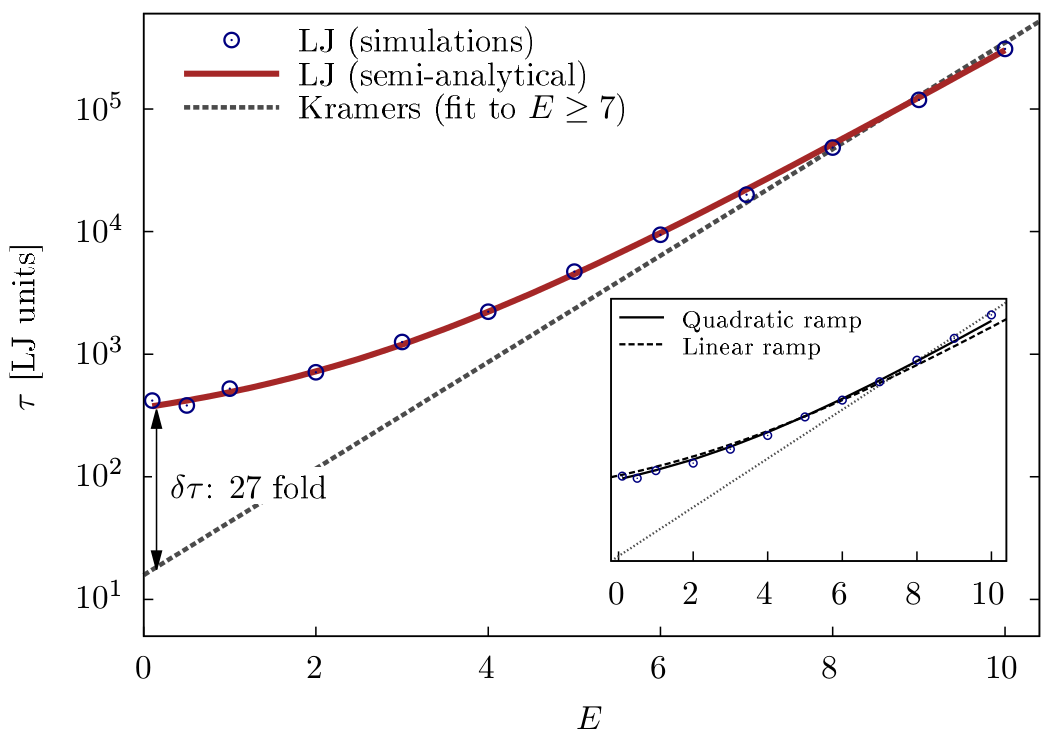
Theories that are used to calculate this mean dissociation time are all invariably based on Kramers’ theory (H. A. Kramers, Physica 7, 284 (1940)). But this theory crucially relies on the assumption that the barrier energy is much larger than thermal fluctuations (E ≫ 1), while for many biological systems this assupmtion might not be true.
Lennard-Jones interaction between two Brownian particles |
Dissociation time as a function of the bond strength. Kramers’ law works well for E ≳ 7, whereas our solutions fit better across the entire range. |
We propose a theoretical framework and extensive numerical simulations which amend Kramers’ theory in the range of E ≈ 1 and use it to extract the dissociation rate from single-molecule experiments where now predictions are physically meaningful and in agreement with simulations over the whole range of applied forces (binding energies).
Related publication
-
Masoud Abkenar, Thomas H. Gray, and Alessio Zaccone. Dissociation rates from single-molecule pulling experiments under large thermal fluctuations or large applied force. Physical Review E 95, no. 4 (2017): 042413.
Interaction of propelled filaments on motility assays
Incomplete
Phase behavior of self-propelled rods with length bidispersity
Incomplete